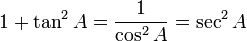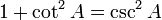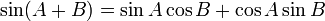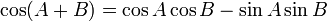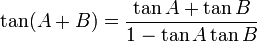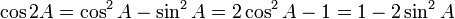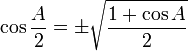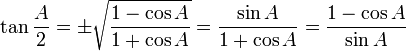Trigonometry is usually taught in secondary schools either as a separate course or as part of a precalculus course. It has applications in both pure mathematics and in applied mathematics, where it is essential in many branches of science and technology. A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomy and navigation.
If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:
- The sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
- The cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
- The tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under Mnemonics).
The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec) and cotangent (cot), respectively. The inverse functions are called the arcsine, arccosine, and arctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities.
With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and an angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.
Extending the definitions
The above definitions apply to angles between 0 and 90 degrees (0 and π/2 radians) only. Using the unit circle, one can extend them to all positive and negative arguments (see trigonometric function). The trigonometric functions are periodic, with a period of 360 degrees or 2π radians. That means their values repeat at those intervals.
The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex function cis is particularly useful
See Euler's and De Moivre's formulas.
Mnemonics
A common use of mnemonics is to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, as in SOH-CAH-TOA.
- Sine = Opposite ÷ Hypotenuse
- Cosine = Adjacent ÷ Hypotenuse
- Tangent = Opposite ÷ Adjacent
The memorization of this mnemonic can be aided by expanding it into a phrase, such as "Some Officers Have Curly Auburn Hair Till Old Age".[4] Any memorable phrase constructed of words beginning with the letters S-O-H-C-A-H-T-O-A will serve.
Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.
Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan and sometimes cis) and their inverses. Most allow a choice of angle measurement methods: degrees, radians and, sometimes, grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built-in instructions for calculating trigonometric functions.
Applications of trigonometry
There is an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
Fields which make use of trigonometry or trigonometric functions include astronomy (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.

Common formulas
Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. There are some identities which equate an expression to a different expression involving the same angles and these are listed in List of trigonometric identities, and then there are the triangle identities which relate the sides and angles of a given triangle and these are listed below.
In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.
Law of sines
The law of sines (also known as the "sine rule") for an arbitrary triangle states:
where R is the radius of the circumcircle of the triangle:
Another law involving sines can be used to calculate the area of a triangle. If you know two sides and the angle between the sides, the area of the triangle becomes:
Law of cosines
The law of cosines ( known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
or equivalently:
Law of tangents
Hubungan fungsi trigonometri
Penjumlahan
Rumus sudut rangkap dua
Rumus sudut rangkap tiga
Rumus setengah sudut
Sinus dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi sinus di atas maka nilai sinus adalah

Nilai sinus positif di kuadran I dan II dan negatif di kuadran III dan IV.
Nilai sinus sudut istimewa
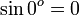



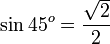

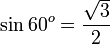
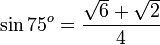

Kosinus
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Kosinus atau cosinus (simbol: cos) dalam matematika adalah perbandingan sisi segitiga yang terletak di sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan. Berdasarkan definisi kosinus di atas maka nilai kosinus adalah

Nilai kosinus positif di kuadran I dan IV dan negatif di kuadran II dan III.
Nilai cosinus sudut istimewa

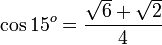
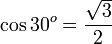

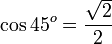


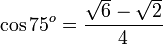

Tangen
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Tangen (bahasa Belanda: tangens; lambang tg, tan) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi tangen di atas maka nilai tangen adalah

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.
Hubungan Nilai Tangen dengan Nilai Sinus dan Cosinus
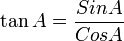
Nilai Tangen Sudut Istimewa







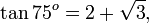










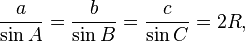
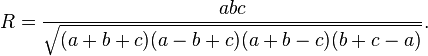
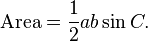
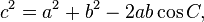

![\frac{a-b}{a+b}=\frac{\tan\left[\tfrac{1}{2}(A-B)\right]}{\tan\left[\tfrac{1}{2}(A+B)\right]}](http://upload.wikimedia.org/math/c/b/5/cb5c755b587d4e4e1f4367c492c4de8d.png)